
sábado, 20 de noviembre de 2010
INFORMATICA EDUCATIVA 2010

lunes, 28 de septiembre de 2009
TEORIA DE CONJUNTO
En matemáticas el concepto de conjunto es considerado primitivo y ni se da una definición de este, sino que se trabaja con la notación de colección y agrupamiento de objetos, lo mismo puede decirse que se consideren primitivas las ideas de elemento y pertenencia.
La característica esencial de un conjunto es la de estar bien definido, es decir que dado un objeto particular, determinar si este pertenece o no al conjunto. Por ejemplo si se considera el conjunto de los números dígitos, sabemos que el 3 pertenece al conjunto, pero el 19 no. Por otro lado el conjunto de las bellas obras musicales no es un conjunto bien definido, puesto que diferentes personas puedan incluir distintas obras en el conjunto.
Los objetos que forman un conjunto son llamados miembros o elementos. Por ejemplo el conjunto de las letras de alfabeto; a, b, c, ..., x, y, z. que se puede escribir así:
{ a, b, c, ..., x, y, z}
Como se muestra el conjunto se escribe entre llaves ({}) , o separados por comas (,).
Los conjuntos se denotan por letras mayúsculas : A, B, C,... por ejemplo:
A={ a, c, b }
B={ primavera, verano, otoño, invierno }
El símbolo Î indicará que un elemento pertenece o es miembro de un conjunto. Por el contrario para indicar que un elemento no pertenece al conjunto de referencia, bastará cancelarlo con una raya inclinada / quedando el símbolo como Ï .
Ejemplo:
Sea B={ a, e, i, o, u }, a Î B y c Ï B
La unión de dos conjuntos A y B la denotaremos por A È B y es el conjunto formado por los elementos que pertenecen al menos a uno de ellos ó a los dos. Lo que se denota por:
A È B = { x/x Î A ó x Î B }
Ejemplo: Sean los conjuntos A={ 1, 3, 5, 7, 9 } y B={ 10, 11, 12 }
A È B ={ 1, 3, 5, 7, 9, 10, 11, 12 }
Sean A={ 1, 2, 3, 4, 5, 6, 8, 9 } y B={ 2, 4, 8, 12 }

Los elementos comunes a los dos conjuntos son: { 2, 4, 8 }. A este conjunto se le llama intersección de A y B; y se denota por A Ç B, algebraicamente se escribe así:
A Ç B = { x/x Î A y x Î B }
Y se lee el conjunto de elementos x que están en A y están en B.
Ejemplo:
Sean Q={ a, n, p, y, q, s, r, o, b, k } y P={ l, u, a, o, s, r, b, v, y, z }
Q Ç P={ a, b, o, r, s, y }
El complemento de un conjunto respecto al universo U es el conjunto de elementos de U que no pertenecen a A y se denota como A' y que se representa por comprehensión como:
A'={ x Î U/x y x Ï A }
Ejemplo:
Sea U = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }
A= { 1, 3, 5, 7, 9 } donde A Ì U
El complemento de A estará dado por:
A'= { 2, 4, 6, 8 }
Sean A y B dos conjuntos. La diferencia de A y B se denota por A-B y es el conjunto de los elementos de A que no están en B y se representa por comprehensión como:
A - B={ x/x Î A ; X Ï B }

Ejemplo:
Sea A= { a, b, c, d } y
B= { a, b, c, g, h, i }
A - B= { d }
En el ejemplo anterior se observa que solo interesan los elementos del conjunto A que no estén en B. Si la operación fuera B - A el resultado es
B – A = { g, h, i }
E indica los elementos que están en B y no en A.
TEORÍA DE DECISIONES

En sentido restrictivo, decidir es seleccionar, entre varias, una y sólo una entidad alternativa. Hay decisión cuando, siendo posible varias respuestas, un sujeto elige una de ellas.En sentido amplio, decidir es llevar a cabo un proceso completo por el cual se establecen, analizan y evalúan alternativas a fin de seleccionar una y sólo una
Teoría de la Decisión
En cuanto a decisión se refiere, existen dos enfoques sobresalientes:
La teoría de la elección racional (Simón): desde una perspectiva descriptiva, nos cuenta
CÓMO SON los procesos decisorios en las organizaciones. Los hombres aplican su propia racionalidad limitada por su singular visión de la realidad.
La teoría de la decisión: es una metodología prescriptiva o normativa que indica CÓMO SE DEBE DECIDIR para ser consecuentes con los objetivos, preferencias y ciertos principios impuestos por la teoría. (cómo se debe decidir, pero no que decidir).
Elementos de un Proceso de Decisión
El decisor (TD): Es el encargado de realizar la selección de alternativas de la mejor manera, en función de sus objetivos
Las alternativas o cursos de acción: son las diferentes formas de actuar posibles: el TD deberá seleccionar una de ellas. Es importante tener en cuenta que estas alternativas deben ser excluyentes entre sí.
Los estados de la naturaleza: son las variables no controlables por el TD. Son eventos futuros que influyen en el proceso de decisión, pero que no pueden ser controladas ni previstas, en su comportamiento, por el TD.
Los resultados: es lo que se obtiene ante la selección (la opción) de una alternativa determinada cuando se presenta uno de los posibles estados de la naturaleza.
Etapas del Proceso Decisorio
1.El TD debe identificar la existencia de un problema y poder definirlo.
2. El TD debe recopilar más información acerca del problema.
3. El TD debe poder especificar los objetivos.
4. El TD debe elaborar un modelo que describa el problema.
5. El TD debe generar soluciones alternativas al problema y evaluarlas en función de sus preferencias (análisis cualitativo y análisis cuantitativo).
6. El TD debe determinar el criterio de decisión que optimice la situación.
7. El TD debe predecir las consecuencias de cada actuación.
8. El TD debe establecer un sistema de preferencias. Tiene que realizar una valoración de las consecuencias de acuerdo con una escala de bondad o deseabilidad.
9. El TD debe elegir entre las soluciones alternativas. Es necesario que seleccione un curso de acción. Esta elección debe darse mediante un criterio de decisión adecuado.
10. El TD debe poner en práctica la solución seleccionada y evaluar los resultados. Lo que modifica el universo, es la acción derivada de la decisión.
¿Qué hacer frente a un problema?
Existen cuatro maneras básicas para tratar un problema:
Absolver un problema consiste en ignorarlo y esperar a que desaparezca o se desenrede solo.
Resolver el problema consiste en tomar alguna acción razonablemente buena, que genere satisfacción.
Solucionar un problema consiste en tomar la mejor acción posible, la que optimiza. Quienes solucionan problemas los enfocan científicamente, se apoyan en especial en la experimentación y en el análisis cuantitativo.
Disolver un problema es eliminarlo rediseñando el sistema que lo incluye. Quienes disuelven problemas tratan de idealizar, esto es, aproximarse a un sistema ideal y, de ese modo, conseguir un desempeño futuro superior al más satisfactorio que pueda obtenerse hoy en día.

Lenguaje artificial compuesto por caracteres de uno o varios tipos (letras y/o números u otros signos gráficos), cargados -cada uno de ellos- con un significado específico en el contexto de un sistema de clasificación. La notación está destinada a representar los conceptos presentes en un sistema de clasificación, y a traducir los asuntos contenidos en los documentos del lenguaje natural al lenguaje codificado del sistema, así como a explicitar las diversas relaciones establecidas entre dicho asuntos.
La notación constituye la base de los sistemas notacionales de clasificación, y se desarrolla generalmente a partir de un orden reconocido (por ej., el de las letras del alfabeto). Asimismo, organiza la ordenación de los encabezamientos temáticos dentro de un catálogo sistemático. Las características esperables en toda notación son: la brevedad, la expresividad, la composición lógica, la legibilidad, la hospitalidad, la flexibilidad y la mnemotecnia. // 2. Símbolo formado a partir de una base notacional, que permite identificar temáticamente y ubicar a un documento en una colección. El símbolo notacional asignado a dicho documento facilita su localización en los estantes y en los catálogos o registros.
Las notaciones son una forma especial en la que se pueden expresar una expresión matemática y puedan ser de 3 formas: infija, prefija y posfija. Los prefijos, Pre - Pos - In se refieren a la posición relativa del operador con respecto a los dos operadnos.
Operadnos1 + 5
INFIJA PREFIJA POSFIJA
NOTACIÓN PREFIJA
Nos indica que el operador va antes de los operando sus características principales son:
-Los operados conservan el mismo orden que la notación infija equivalente.
-No requiere de paréntesis para indicar el orden de precedencia de operadores ya que él es una operación.Se evalúa de izquierda a derecha hasta que encontrémosle primer operador seguido mediatamente de un par de operandos. Se evalúa la expresión binaria y el resultado se cambia como un nuevo operando. Se repite este hasta que nos quede un solo resultado.
NOTACION POSFIJA
Como su nombre lo indica se refiere a que el operador ocupa la posición después de los operandos sus características principales son: el orden de los operandos se conserva igual que la expresión infija equivalente no utiliza paréntesis ya que no es una operación ambigua.
-La operación posfija no es exactamente lo inverso a la operación prefija equivalente:
NOTACION INFIJA
Es la forma más común que utilizamos para escribir expresiones matemáticas, estas notaciones se refiere a que el operador está entre los operandos. La notación infija puede estar completamente patentizada o puede basarse en un esquema de precedencia de operadores así como el uso de paréntesis para invalidar los arreglos al expresar el orden de evaluación de una expresión:
3*4+2=14
3*(4+2)=18
DIAGRAMAS FORRESTER.

La estructura básica contiene cuatro características principales:
 Varios niveles.
Varios niveles.Flujos que transportan el contenido de un nivel a otro.
Funciones de Decisión (dibujadas como válvulas) que controlan la rapidez de los flujos entre los niveles.
Canales de información que conectan las funciones de decisión a los niveles.
Función de Decisión
Canal de Flujo
Fuentes de información
Variable Auxiliar
Límite del Sistema
Variable de nivel: constituyen un conjunto de variables cuya evolución es significativa para el estudio del sistema.
Variable de flujo: determinan los cambios en las variables de nivel en el sistema. Las variables de flujo caracterizan las acciones que se toman en el sistema, las cuales queda acumuladas en los correspondientes niveles.
Variable auxiliar: representa pasos o etapas en que se pone el cálculo de una variable de flujo a partir de los valores representados por los estados de la variable de nivel. Las variables aux unen los canales de información entre las de nivel y de flujo, aunque en realidad son parte de las variables de flujo. Sin embargo se distinguen de ellas en la medida que su significado real sea más explícito.
Variable constante: representa un elemento en el modelo que no cambia a medida que el tiempo cambia.
Canal de material: es un canal de transmisión de una magnitud física que se conserva, de tal manera que los niveles siempre acumulan flujos de materiales.
Canal de información: Canal de transmisión de una cierta información y no es factible que esta se conserve.
Retraso: es un elemento que simula retrasos en la transmición de información o de materiales.
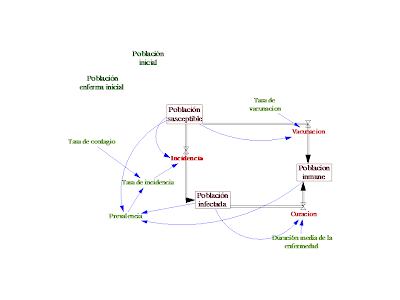
Diagrama de estados
En cuanto a la representación, un diagrama de estados es un grafo cuyos nodos son estados y cuyos arcos dirigidos son transiciones etiquetadas con los nombres de los eventos. Un estado se representa como una caja redondeada con el nombre del estado en su interior. Una transición se representa como una flecha desde el estado origen al estado destino.

La caja de un estado puede tener 1 o 2 compartimentos. En el primer compartimento aparece el nombre del estado. El segundo compartimento es opcional, y en él pueden aparecer acciones de entrada, de salida y acciones internas. Una acción de entrada aparece en la forma entrada/acción asociada donde acción asociada es el nombre de la acción que se realiza al entrar en ese estado. Cada vez que se entra al estado por medio de una transición la acción de entrada se ejecuta.

Una acción de salida aparece en la forma salida/acción asociada. Cada vez que se sale del estado por una transición de salida la acción de salida se ejecuta.
Una acción interna es una acción que se ejecuta cuando se recibe un determinado evento en ese estado, pero que no causa una transición a otro estado. Se indica en la forma nombre_de_evento/acción_asociada.

SEUDOCODIGOS

El pseudocódigo describe un algoritmo utilizando una mezcla de frases en lenguaje común, instrucciones de programación y palabras clave que definen las estructuras básicas. Su objetivo es permitir que el programador se centre en los aspectos lógicos de la solución a un problema.
La relación de convenciones empleadas en el pseudocódigo es la siguiente: El pseudocódigo se escribe empleando la fuente Times New Román Las palabras reservadas del pseudocódigo se muestran en negritas.
Los puntos "..." indican la posibilidad de repetir algún elemento del pseudocódigo.
Cuando exista la posibilidad de elegir algún elemento a partir de un conjunto de elementos, éstos se listarán separados por el símbolo "".
Las diferentes opciones o posibilidades de uso del pseudocódigo se listan con viñetas.
CARACTERISTICAS DE LOS SEUDOCODIGOS
Se emplean oraciones en lenguaje natural, donde cada una se refiere a una actividad general o específica.
Se utiliza un lenguaje común, sin palabras rebuscadas.
Se evitan errores gramaticales.
Tipos de datos
Los tipos de datos básicos son:
string cadena de caracteres.
integer número entero.
real número real.
booleana falso o verdadero.
Operadores Aritméticos:
+ Suma
- Resta
* Multiplicación
/ División
mod módulo
div división entera
De comparación
= igual <> Diferente
<> Mayor que
<= menor o igual que >= mayor o igual que
Lógicos
AND La expresión será verdadera si y sólo si ambas expresiones son verdaderas
OR La expresión será verdadera si al menos una expresión es verdadera
XOR La expresión será verdadera si y sólo si ambas expresiones son diferentes (verdadero y falso, o viceversa)
NOT El valor de la expresión es la negación de la expresión original.


